Floating point data

Floating point (FP) data is a common way to store real numbers (R). Many different types of floating point data types exist, but the most relevant types for scientific computing are:

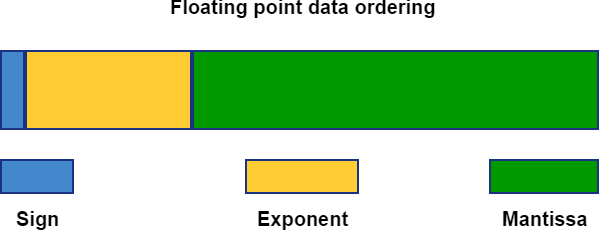
Floating point data contains three parts, the sign, the exponent and the mantissa. The sign and exponent are both stored as 2-base little-endian (most significant bit to the left) numbers. The mantissa is treated slightly differently. It is stored as a 2-base big-endian number (most significant bit to the right) with an implicit least significant bit equated to 0.

Floating point

Generic 2-base number example:

2 base sign/exponent = $ 0111 $

10 base sign/exponent = $ (8 \times 0) + (4 \times 1) + (2 \times 1) + (1 \times 1) $ = $ 7 $

2 base mantissa = $ 0111 $

10 base mantissa = $ (1 \times 0) + (2 \times 0) + (4 \times 1) + (8 \times 1) + (16 \times 1) $ = $ 28 $

Generic calculation floating point value:

Value = $ -1^{Sign_{2}} \times 2^{Exponent_{10} - Bias_{10}} \times (1 + 1/(Mantissa_{10})) $

Bias is a datatype specific number to “center” the exponent range around 0.

Double (64 bit):

Common format for sensitive mathematical equations, like solving ill conditioned systems. Default data type of MATLAB.

Resolution: $ (1/2)^{52} = 2.2204e-16 $

Exponent range: $ 2^{([-1023,1024])} $

Single (32 bit):

Original floating point data type used in 32 bit computers, provides sufficient resolution for many mathematical operations.

Resolution: $ (1/2)^{23} = 1.1921e-07 $

Exponent range: $ 2^{([-127,128])} $

Half (16 bit):

Relatively coarse approximation of a real number, but sometimes good enough. A great example of applications that usually don’t require more precision are deep neural networks.

Resolution: $ (1/2)^{10} = 9.7656e-04 $

Exponent range: $ 2^{([-15,16])} $

Floating point operation: Fused Multiply Add (FMA)

The prolific nature of the dot product in vector mathematics has lead to the development of hardware dedicated to the task, performing a multiplication and addition in a single step:

A = A + B x C

It should be noted that the FMA operation can be used to emulate (may take more then a single instruction) the basic operations:

As such, most modern computers rely on FMA hardware for all their floating point calculations. The low level hardware required to perform the FMA calculation, differs for every floating point format (double, single or half). This makes it a common practice provide separate hardware blocks for each floating point format.